MICROTUNING AND ALTERNATIVE INTONATION SYSTEMS
MICROTUNING VIRTUAL AND ELECTRONIC HARDWARE INSTRUMENTS: AN OVERVIEW OF FORMATS AND METHODS FOR USING ALTERNATIVE INTONATION SYSTEMS
For those electronic hardware synthesis enthusiasts, as well as computer based musicians and composers who wish to explore the vast expressive possibilities, new harmonies and melodic potentials of using alternative intonation systems in their music creation processes (just intonation, temperaments, non-octave, historical microtunings, etc.), they will inevitably face the complexity of dealing with the different kinds of popular microtuning formats, including: various types of tuning tables, MIDI SYSEX, scripts, etc., required for retuning their hardware and software instruments.
Since there currently are no universal methods for changing the intonation of electronic musical instruments, the task for microtuning ensembles of virtual or hardware instruments to a single intonation system, much less a dynamic intonation environment, can often be a daunting chore for newcomers to the field of xenharmonic and microtonal music composition.
The primary concern of this short article are music software and hardware developers who offer products that feature what is often referred to as full-controller, or otherwise, full-keyboard microtuning, and some of the currently popular methods for changing their underlying intonation to tuning systems other than the well-worn and ubiquitous 12-tone-equal-temperament that has been the defacto standard in Western music since the 19th century.
Essentially, full-keyboard microtuning gives musicians and composers complete, unrestricted control over how the pitches of intonation systems are directly mapped to MIDI Notes on their controllers, and enables mappings that can have less, or greater than 12 notes that repeat across the range of the instrument, as well as allowing the use of systems that have repeat intervals other than the typical 2/1 octave at 1200 cents.
Among the ways that the complexity of microtuning ‘format overload’ may manifest for electronic musicians and composers are as follows:
Buyer beware and be informed: There are a bewildering number of different microtuning implementations…
12 Note Octave Repeating Microtuning
Some virtual and hardware instruments, as well as some DAWs (for example, Alchemy, and the other virtual instruments featured in Apple Logic), may only permit retuning 12 pitches within a 2/1 octave boundary of 1200 cents. It’s important to recognize that although these instruments may be capable of generating a huge range of amazing timbres and sound-designs, this restricted kind of tuning implementation is not capable of full-controller, or full-keyboard microtuning, and therefore has far less utility for serious microtonal and xenharmonic music composition, since their design remains locked into thinking about musical instrument intonation in terms of 12 octave-bound notes repeated across the musical range, and are therefore incapable of being used for intonation systems that feature more or less than 12 notes, or otherwise ones that may not repeat at the interval of octave at all.
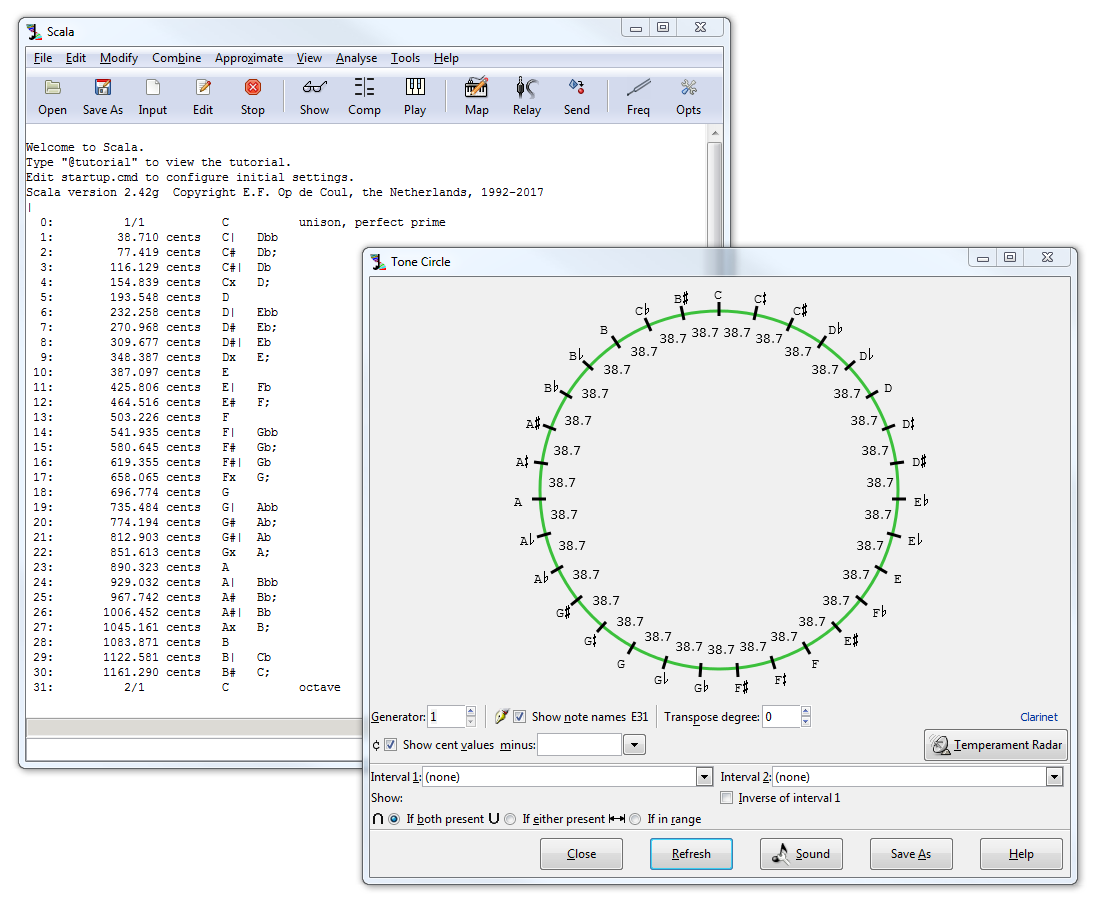
Among the many possible examples, 12 Note Octave Repeating Microtuning would prohibit the use of such popular microtunings as Bohlen-Pierce, which divides the 3rd harmonic into 13 equal parts and has a repeat interval of a 3/1 at 1901.955 cents:
Bohlen-Pierce: ED3-13 – Equal division of harmonic 3 into 13 parts
0: 1/1 0.000000 unison, perfect prime
1: 146.304 cents 146.304230
2: 292.608 cents 292.608460
3: 438.913 cents 438.912690
4: 585.217 cents 585.216920
5: 731.521 cents 731.521150
6: 877.825 cents 877.825390
7: 1024.130 cents 1024.129620
8: 1170.434 cents 1170.433850
9: 1316.738 cents 1316.738080
10: 1463.042 cents 1463.042310
11: 1609.347 cents 1609.346540
12: 1755.651 cents 1755.650770
13: 3/1 1901.955001 perfect 12th
The restriction of 12 Note Octave Repeating Microtuning would also preclude the use of the famous Wendy Carlos, Alpha (78 cents step size), Beta (63.8 cents step size) and Gamma (35.1 cents step size) systems, none of which feature a repeat interval of a 2/1 (Tuning: At the Crossroads, Computer Music Journal, Vol. 11, No. 1, Microtonality, Spring, 1987).
There are countless other such examples of historical and contemporary musical instrument intonation systems that would be able to easily illustrate the glaring shortcomings of being restricted to only 12 notes repeating at the 2/1. For musicians and composers to be able to encompass the full range of expression and compositional possibilities of using alternative intonation systems in their music – including, but not limited to, 12 Note Octave Repeating Microtunings – it is advised to support those visionary developers who have implemented full-keyboard microtuning in their instruments. With correctly implemented full-keyboard microtuning functionality, there is no compromise in the way that one may microtune their hardware or virtual instruments.
The Scala SCL/KBM Specification
Some microtuning implementations may allow retuning instruments with more or less than 12 tones, but provide no uniform method for independently configuring the Key For 1/1 (the MIDI Note on which the microtuning will start) and Reference Frequency (the MIDI Note on which the reference pitch will be mapped, for example, the concert standard of 69.A at 440 Hz). Such is the case with the widespread implementation of the Scala SCL format, where the linear KBM (keyboard mapping) part of the standard has been omitted, a topic which we will explore more in depth ahead.
Native Instruments Kontakt Script Language: KSP
Native Instruments Kontakt, which in theory enables full-controller microtuning, may have encrypted commercial sample libraries that strictly prohibit changing the intonation with its KSP scripting language. Moreover, KSP scripts may be used for sophisticated key-switching, or other such articulation schemes, that might prevent using a full-keyboard microtuning KSP script at the same time. Users of Kontakt should be fully prepared and equipped to program their own KSP scripts, sample instruments and libraries to ensure that they can be fully microtuned, as many developers of Kontakt libraries may not be empathetic to the requirements of microtonal and xenharmonic music composition, and very well may have designed their instruments with no, or extremely limited, ability for full-keyboard microtuning with the KSP language. In other words, they may be entirely ’12-locked’, and incapable of rendering music with intonation systems other than 12-tone-equal-temperament.
Full-Keyboard Microtuning: TUN and MTS Formats
Virtual instruments that can more easily achieve high-precision full-controller microtuning are those where developers have implemented the use of either the TUN or MTS (MIDI Tuning Standard) microtuning formats, which enable saving all of the microtuning mapping information into a single tuning data file that may be loaded directly into the instruments, or in the case of MTS, also be transmitted from the timeline of DAWs that allow transmitting SYSEX, such as for example REAPER and Bitwig.
Microtonal music software developers may have their own unique data-management strategies for working with microtuning files.
Some developers may have designed their microtonal software synthesizers and samplers so that microtuning format files may be loaded into their virtual instruments from any directories on the user’s computers, which empowers computer musicians and composers to use and maintain a single centralized global microtuning directory for all virtual instruments, while others may require that the microtuning data files be stored within the plugin’s directory.
Where developers have employed the latter method of requiring users to store microtuning files within the plugin’s directory only, and do not permit loading them from any directory on the computer; this will require that users of the software maintain multiple concurrent microtuning archives for each plugin that uses this method, such as in the case of the excellent u-he virtual instrument line (Diva, Zebra, Bazille, ACE), thereby adding another layer of complexity for working with microtunings and managing the tuning file data.
Microtuning Formats: A Closer Look
Let’s more closely consider here some of the currently popular methods for microtuning computer music based virtual instruments and some hardware instruments, with this brief overview of their features and benefits:
TUN
The TUN format, invented by visionary developer, Mark Henning, is currently among the most popular and widely used microtuning formats for computer music virtual instruments. He is also the developer of the AnaMark VSTi synthesizer, which was first published with TUN support on February 19, 2003, making it among the earliest VSTi supporting full-controller microtuning tables. The TUN format is an elegant solution for retuning MIDI controlled virtual instruments to alternative intonation systems, because both the MIDI Note Number on which the 1/1 starting note of the microtuning will be placed, as well as the MIDI Note Number on which the Reference Frequency will be mapped, can be freely and independently specified, and is embedded within a single text file that is read by the instrument.
Pros:
- TUN is a high precision microtuning-table text format that includes the scale and MIDI Note mapping information in cents.
- Users can specify both the Key For 1/1 (the MIDI Note on which the microtuning will start) and Reference Frequency (the MIDI Note on which the reference pitch will be mapped, for example, the standard concert pitch of 69.A at 440 Hz). Typically these critical parameters are configured and the data exported using dedicated microtuning applications such as Scala, which enables users to save versions of scales with different mappings as required of the music at hand.
- Virtual instruments can be fully microtuned using a single TUN file.
- Human readable with a text editor.
Cons:
- No dynamic, real-time microtuning.
- To change to other intonation systems, a new TUN file must be manually loaded by the user for every instrument being used in a composition that requires it.
Some virtual instrument software developers that have implemented the TUN microtuning format in their products: Big Tick, Linplug, MeldaProduction, Plugin Boutique, Rob Papen, Robin Schmidt, Spectrasonics, TAL Software, u-he, VAZ Synths, Xfer Records.
Scala SCL/KBM
Also popular is the SCL/KBM format from the developer of the versatile Scala microtuning application, Manuel Op de Coul, and is an excellent and flexible text based format that is ideal for archiving intonation systems, which may be expressed in ratios and or cents.
Pros:
- Virtual instruments can be fully microtuned using both the SCL and linear KBM files. SCL is the part of the standard that contains the intervals of the scale, while the linear KBM part is what determines how the pitches are mapped directly to MIDI Notes on the controller.
- Human readable with a text editor.
- The Key For 1/1 (the MIDI Note on which the microtuning will start) and Reference Frequency (the MIDI Note on which the reference pitch will be mapped, e.g., the standard concert pitch of 69.A at 440 Hz) can be independently specified and freely changed using the linear KBM (Keyboard Mapping File).
Cons:
- No dynamic, real-time microtuning.
- To change to another intonation system, a new SCL and a linear KBM file must be manually loaded by the user for every instrument.
An important note regarding the Scala SCL/KBM format
Both the SCL and linear KBM parts of the Scala specification are required to achieve full-controller microtuning and provide users the ability to fluidly change how intonation systems are mapped to their controllers. The reality is that very few developers have correctly implemented both SCL and linear KBM functionality, so where instruments are only able to load the SCL file, without the linear KBM part, it may not always be possible to independently change the Key For 1/1 (the starting MIDI Note of the microtuning) and the Reference Frequency (the MIDI Note on which the reference pitch will be mapped, e.g., the standard concert pitch of 69.A at 440 Hz).
Often, without the ability to load the linear KBM files, such as in the case of the Cakewalk and Image Line virtual instruments, Reveal Sound‘s Spire, and all of the Applied Acoustics VSTi (sadly, their great sounding Chromophone physical modeling instrument included), which use only the SCL part of the Scala specification without the linear KBM, the Key For 1/1 and the Reference Frequency are often treated as one in the same. Other such worst-case-scenario implementations of SCL may map any loaded microtunings to start on middle C (MIDI Note 60.C), and provide no convenient method for changing the mapping of an intonation system at all.
For example, it would be virtually impossible in these virtual instruments to load a Scala SCL microtuning and have the Key For 1/1 start on MIDI Note 60.C, and at the same time have the Reference Frequency on MIDI Note 69.A @ 440 Hz, because, without the KBM file, the Key For 1/1 and Reference Frequency are configured by a single parameter: set the reference note to 69.A 440 Hz, and both the Key For 1/1 and Reference Frequency are mapped on MIDI Note 69.A @ 440 Hz. Likewise, when setting the reference note to 60.C @ 261.625565 Hz, both the Key For 1/1 and Reference Frequency for the microtuning are mapped on 60.C @ 261.625565 Hz. This may be all well and fine for many Equal Temperaments, but with a universe of other types of intonation systems that feature different step sizes and intervals under modal rotation (MOS, just intonation, microtonal-modes-of-limited-transposition, etc.), the SCL-without-KBM microtuning mapping paradigm immediately fails to be able to accurately render microtunings with discrete Key-for-1/1 and Reference Frequency parameters, and will not sound in tune with ensembles of instruments that are microtuned this in this manner.
As we can see, in cases where developers have naively omitted the linear KBM part of the Scala specification, this causes a huge complication for musicians and composers endeavoring to easily microtune ensembles of virtual instruments to a common intonation system, where the requirements of specialized MIDI controller mappings, as well as the music at hand, are that the Key For 1/1 and Reference Frequency need to be independently specified for all of the instruments being used in a particular microtonal or xenharmonic compositional scenario.
The ability to freely map these two parameters of microtunings becomes especially critical when working with various kinds of hexagonal array keyboards, such as the Starr Labs Microzone U-648 Generalized Keyboard, C-Thru Music AXis-64 and AXis-49, as well as grid-based MIDI controllers like the excellent Roger Linn Design LinnStrument and the Novation LaunchPad Pro. It would also be crucial for mapping microtonal tunings to Elaine Walker’s Vertical Keyboards, which feature Halberstadt-style MIDI key-beds with customized key arrangements that are designed to accommodate a wide range of microtonal tunings and ergonomic fingering requirements.
There is hope: Modartt Pianoteq gets it right
Among the most elegant (and correct) implementations of the Scala SCL and linear KBM microtuning format, is found in the excellent physical modeling Modartt Pianoteq virtual instrument, which enables musicians and composers to directly load both Scala SCL microtunings and the KBM Keyboard Mapping files from its user interface.
Below are a couple of linear KBM file examples to illustrate the microtuning mapping flexibility embodied in the Modartt Pianoteq implementation of the Scala SCL/KBM specification:
60-440-69.kbm | This KBM file would place the Key For 1/1 on MIDI Note 60.C, while mapping the Reference Frequency to MIDI Note 69.A at a frequency of 440 Hz:
! 60-440-69.kbm
!
! Size of map:
0
! First MIDI note number to retune:
0
! Last MIDI note number to retune:
127
! Middle note where the first entry in the mapping is mapped to:
60
! Reference note for which frequency is given:
69
! Frequency to tune the above note to (floating point e.g. 440.0):
440.000000
! Scale degree to consider as formal octave:
0
! Mapping.
52-262-60.kbm | Here the KBM file would place the Key For 1/1 on MIDI Note 52.E, while mapping the Reference Frequency to MIDI Note 60.C at a frequency of 261.625565 Hz:
! 52-262-60.kbm
!
! Size of map:
0
! First MIDI note number to retune:
0
! Last MIDI note number to retune:
127
! Middle note where the first entry in the mapping is mapped to:
52
! Reference note for which frequency is given:
60
! Frequency to tune the above note to (floating point e.g. 440.0):
261.625565
! Scale degree to consider as formal octave:
0
! Mapping.
When advocating for the Scala microtuning format…
Let’s hope that this information will help to illuminate the issues around full-keyboard microtuning with Scala files, as well as to inspire musicians and composers advocating for the Scala SCL format to include the crucial KBM part in their advocacy, and that developers will see how critically important the combination and correct implementation of both the SCL and linear KBM parts of the Scala specification are to serious microtonal and xenharmonic music composition.
Some virtual instrument software developers that have correctly implemented the Scala SCL/KBM format in their products: Modartt Pianoteq, ZynAddSubFX 2.4.1, amSynth (Linux), UVI.
MTS (MIDI Tuning Standard)
The MIDI Tuning Standard is an ultra-high-resolution specification for microtuning MIDI instruments agreed upon by the MIDI Manufacturers Association, and was developed by visionary microtonal music composers Robert Rich and Carter Scholz. The standard includes both Bulk Dump and Single Note microtuning with a resolution of 0.0061 cent, which essentially divides the octave into 196,608 equal parts. It remains among the best and most flexible real-time microtuning formats available today.
Pros:
- Virtual instruments can be fully microtuned using single MTS files.
- Has been a part of the MIDI Specification since the 1990s.
- Single, as well as entire ensembles of virtual instruments, can be fully and dynamically microtuned in real-time within DAWs, or using sequencers, that support the transmission of MIDI SYSEX data to instruments, without the need to manually load new microtuning files by hand in the manner required with TUN and SCL/KBM.
Cons:
- The format is MIDI SYSEX data, and therefore is not human-readable.
Some virtual instrument software and hardware developers that have implemented the MTS microtuning format in their products: Dave Smith Instruments, E-mu, Ensoniq, Native Instruments, MOTM, Synthogy, Tubbutec, WayOutWare, Xen-Arts, Yamaha.
An important consideration and current reality for the MTS format, is that not all DAWs (Digital Audio Workstations) allow the transmission of MIDI SYSEX to plugins from their timelines, although some, such as REAPER and Bitwig do. Also, the new VST3 format has tragically dropped a lot of the MIDI functionality that was among the most fascinating possibilities of the VST 2.4 SDK, rendering VST3 a huge unknown factor in the future of microtuning virtual instruments.
MIDI Note Number-Hertz-Cents and Octave Table
| MIDI Note Number |
Hz | Cents | MIDI Standard | ISO 16:1975 | Cakewalk |
| Middle C: C3 | Middle C: C4 | Middle C: C5 | |||
| 0 | 8.176 | 0 | C -2 | C -1 | C 0 |
| 1 | 8.662 | 100 | C#, Db -2 | C#, Db -1 | C#, Db 0 |
| 2 | 9.177 | 200 | D -2 | D -1 | D 0 |
| 3 | 9.723 | 300 | D#, Eb -2 | D#, Eb -1 | D#, Eb 0 |
| 4 | 10.301 | 400 | E -2 | E -1 | E 0 |
| 5 | 10.913 | 500 | F -2 | F -1 | F 0 |
| 6 | 11.562 | 600 | F#, Gb -2 | F#, Gb -1 | F#, Gb 0 |
| 7 | 12.25 | 700 | G -2 | G -1 | G 0 |
| 8 | 12.978 | 800 | G#, Ab -2 | G#, Ab -1 | G#, Ab 0 |
| 9 | 13.75 | 900 | A -2 | A -1 | A 0 |
| 10 | 14.568 | 1000 | A#, Bb -2 | A#, Bb -1 | A#, Bb 0 |
| 11 | 15.434 | 1100 | B -2 | B -1 | B 0 |
| 12 | 16.352 | 1200 | C -1 | C 0 | C 1 |
| 13 | 17.324 | 1300 | C#, Db -1 | C#, Db 0 | C#, Db 1 |
| 14 | 18.354 | 1400 | D -1 | D 0 | D 1 |
| 15 | 19.445 | 1500 | D#, Eb -1 | D#, Eb 0 | D#, Eb 1 |
| 16 | 20.602 | 1600 | E -1 | E 0 | E 1 |
| 17 | 21.827 | 1700 | F -1 | F 0 | F 1 |
| 18 | 23.125 | 1800 | F#, Gb -1 | F#, Gb 0 | F#, Gb 1 |
| 19 | 24.5 | 1900 | G -1 | G 0 | G 1 |
| 20 | 25.957 | 2000 | G#, Ab -1 | G#, Ab 0 | G#, Ab 1 |
| 21 | 27.5 | 2100 | A -1 | A 0 | A 1 |
| 22 | 29.135 | 2200 | A#, Bb -1 | A#, Bb 0 | A#, Bb 1 |
| 23 | 30.868 | 2300 | B -1 | B 0 | B 1 |
| 24 | 32.703 | 2400 | C 0 | C 1 | C 2 |
| 25 | 34.648 | 2500 | C#, Db 0 | C#, Db 1 | C#, Db 2 |
| 26 | 36.708 | 2600 | D 0 | D 1 | D 2 |
| 27 | 38.891 | 2700 | D#, Eb 0 | D#, Eb 1 | D#, Eb 2 |
| 28 | 41.203 | 2800 | E 0 | E 1 | E 2 |
| 29 | 43.654 | 2900 | F 0 | F 1 | F 2 |
| 30 | 46.249 | 3000 | F#, Gb 0 | F#, Gb 1 | F#, Gb 2 |
| 31 | 48.999 | 3100 | G 0 | G 1 | G 2 |
| 32 | 51.913 | 3200 | G#, Ab 0 | G#, Ab 1 | G#, Ab 2 |
| 33 | 55 | 3300 | A 0 | A 1 | A 2 |
| 34 | 58.27 | 3400 | A#, Bb 0 | A#, Bb 1 | A#, Bb 2 |
| 35 | 61.735 | 3500 | B 0 | B 1 | B 2 |
| 36 | 65.406 | 3600 | C 1 | C 2 | C 3 |
| 37 | 69.296 | 3700 | C#, Db 1 | C#, Db 2 | C#, Db 3 |
| 38 | 73.416 | 3800 | D 1 | D 2 | D 3 |
| 39 | 77.782 | 3900 | D#, Eb 1 | D#, Eb 2 | D#, Eb 3 |
| 40 | 82.407 | 4000 | E 1 | E 2 | E 3 |
| 41 | 87.307 | 4100 | F 1 | F 2 | F 3 |
| 42 | 92.499 | 4200 | F#, Gb 1 | F#, Gb 2 | F#, Gb 3 |
| 43 | 97.999 | 4300 | G 1 | G 2 | G 3 |
| 44 | 103.826 | 4400 | G#, Ab 1 | G#, Ab 2 | G#, Ab 3 |
| 45 | 110 | 4500 | A 1 | A 2 | A 3 |
| 46 | 116.541 | 4600 | A#, Bb 1 | A#, Bb 2 | A#, Bb 3 |
| 47 | 123.471 | 4700 | B 1 | B 2 | B 3 |
| 48 | 130.813 | 4800 | C 2 | C 3 | C 4 |
| 49 | 138.591 | 4900 | C#, Db 2 | C#, Db 3 | C#, Db 4 |
| 50 | 146.832 | 5000 | D 2 | D 3 | D 4 |
| 51 | 155.563 | 5100 | D#, Eb 2 | D#, Eb 3 | D#, Eb 4 |
| 52 | 164.814 | 5200 | E 2 | E 3 | E 4 |
| 53 | 174.614 | 5300 | F 2 | F 3 | F 4 |
| 54 | 184.997 | 5400 | F#, Gb 2 | F#, Gb 3 | F#, Gb 4 |
| 55 | 195.998 | 5500 | G 2 | G 3 | G 4 |
| 56 | 207.652 | 5600 | G#, Ab 2 | G#, Ab 3 | G#, Ab 4 |
| 57 | 220 | 5700 | A 2 | A 3 | A 4 |
| 58 | 233.082 | 5800 | A#, Bb 2 | A#, Bb 3 | A#, Bb 4 |
| 59 | 246.942 | 5900 | B 2 | B 3 | B 4 |
| 60 | 261.626 | 6000 | C 3 | C 4 | C 5 |
| 61 | 277.183 | 6100 | C#, Db 3 | C#, Db 4 | C#, Db 5 |
| 62 | 293.665 | 6200 | D 3 | D 4 | D 5 |
| 63 | 311.127 | 6300 | D#, Eb 3 | D#, Eb 4 | D#, Eb 5 |
| 64 | 329.628 | 6400 | E 3 | E 4 | E 5 |
| 65 | 349.228 | 6500 | F 3 | F 4 | F 5 |
| 66 | 369.994 | 6600 | F#, Gb 3 | F#, Gb 4 | F#, Gb 5 |
| 67 | 391.995 | 6700 | G 3 | G 4 | G 5 |
| 68 | 415.305 | 6800 | G#, Ab 3 | G#, Ab 4 | G#, Ab 5 |
| 69 | 440 | 6900 | A 3 | A 4 | A 5 |
| 70 | 466.164 | 7000 | A#, Bb 3 | A#, Bb 4 | A#, Bb 5 |
| 71 | 493.883 | 7100 | B 3 | B 4 | B 5 |
| 72 | 523.251 | 7200 | C 4 | C 5 | C 6 |
| 73 | 554.365 | 7300 | C#, Db 4 | C#, Db 5 | C#, Db 6 |
| 74 | 587.33 | 7400 | D 4 | D 5 | D 6 |
| 75 | 622.254 | 7500 | D#, Eb 4 | D#, Eb 5 | D#, Eb 6 |
| 76 | 659.255 | 7600 | E 4 | E 5 | E 6 |
| 77 | 698.456 | 7700 | F 4 | F 5 | F 6 |
| 78 | 739.989 | 7800 | F#, Gb 4 | F#, Gb 5 | F#, Gb 6 |
| 79 | 783.991 | 7900 | G 4 | G 5 | G 6 |
| 80 | 830.609 | 8000 | G#, Ab 4 | G#, Ab 5 | G#, Ab 6 |
| 81 | 880 | 8100 | A 4 | A 5 | A 6 |
| 82 | 932.328 | 8200 | A#, Bb 4 | A#, Bb 5 | A#, Bb 6 |
| 83 | 987.767 | 8300 | B 4 | B 5 | B 6 |
| 84 | 1046.502 | 8400 | C 5 | C 6 | C 7 |
| 85 | 1108.731 | 8500 | C#, Db 5 | C#, Db 6 | C#, Db 7 |
| 86 | 1174.659 | 8600 | D 5 | D 6 | D 7 |
| 87 | 1244.508 | 8700 | D#, Eb 5 | D#, Eb 6 | D#, Eb 7 |
| 88 | 1318.51 | 8800 | E 5 | E 6 | E 7 |
| 89 | 1396.913 | 8900 | F 5 | F 6 | F 7 |
| 90 | 1479.978 | 9000 | F#, Gb 5 | F#, Gb 6 | F#, Gb 7 |
| 91 | 1567.982 | 9100 | G 5 | G 6 | G 7 |
| 92 | 1661.219 | 9200 | G#, Ab 5 | G#, Ab 6 | G#, Ab 7 |
| 93 | 1760 | 9300 | A 5 | A 6 | A 7 |
| 94 | 1864.655 | 9400 | A#, Bb 5 | A#, Bb 6 | A#, Bb 7 |
| 95 | 1975.533 | 9500 | B 5 | B 6 | B 7 |
| 96 | 2093.005 | 9600 | C 6 | C 7 | C 8 |
| 97 | 2217.461 | 9700 | C#, Db 6 | C#, Db 7 | C#, Db 8 |
| 98 | 2349.318 | 9800 | D 6 | D 7 | D 8 |
| 99 | 2489.016 | 9900 | D#, Eb 6 | D#, Eb 7 | D#, Eb 8 |
| 100 | 2637.02 | 10000 | E 6 | E 7 | E 8 |
| 101 | 2793.826 | 10100 | F 6 | F 7 | F 8 |
| 102 | 2959.955 | 10200 | F#, Gb 6 | F#, Gb 7 | F#, Gb 8 |
| 103 | 3135.963 | 10300 | G 6 | G 7 | G 8 |
| 104 | 3322.438 | 10400 | G#, Ab 6 | G#, Ab 7 | G#, Ab 8 |
| 105 | 3520 | 10500 | A 6 | A 7 | A 8 |
| 106 | 3729.31 | 10600 | A#, Bb 6 | A#, Bb 7 | A#, Bb 8 |
| 107 | 3951.066 | 10700 | B 6 | B 7 | B 8 |
| 108 | 4186.009 | 10800 | C 7 | C 8 | C 9 |
| 109 | 4434.922 | 10900 | C#, Db 7 | C#, Db 8 | C#, Db 9 |
| 110 | 4698.636 | 11000 | D 7 | D 8 | D 9 |
| 111 | 4978.032 | 11100 | D#, Eb 7 | D#, Eb 8 | D#, Eb 9 |
| 112 | 5274.041 | 11200 | E 7 | E 8 | E 9 |
| 113 | 5587.652 | 11300 | F 7 | F 8 | F 9 |
| 114 | 5919.911 | 11400 | F#, Gb 7 | F#, Gb 8 | F#, Gb 9 |
| 115 | 6271.927 | 11500 | G 7 | G 8 | G 9 |
| 116 | 6644.875 | 11600 | G#, Ab 7 | G#, Ab 8 | G#, Ab 9 |
| 117 | 7040 | 11700 | A 7 | A 8 | A 9 |
| 118 | 7458.62 | 11800 | A#, Bb 7 | A#, Bb 8 | A#, Bb 9 |
| 119 | 7902.133 | 11900 | B 7 | B 8 | B 9 |
| 120 | 8372.018 | 12000 | C 8 | C 9 | C 10 |
| 121 | 8869.844 | 12100 | C#, Db 8 | C#, Db 9 | C#, Db 10 |
| 122 | 9397.273 | 12200 | D 8 | D 9 | D 10 |
| 123 | 9956.063 | 12300 | D#, Eb 8 | D#, Eb 9 | D#, Eb 10 |
| 124 | 10548.082 | 12400 | E 8 | E 9 | E 10 |
| 125 | 11175.303 | 12500 | F 8 | F 9 | F 10 |
| 126 | 11839.822 | 12600 | F#, Gb 8 | F#, Gb 9 | F#, Gb 10 |
| 127 | 12543.854 | 12700 | G 8 | G 9 | G 10 |